1. 먼저 간선을 가중치 값으로 오름차순으로 정렬한다.

2. 간선을 선택해가면서 싸이클이 되어버리면 선택하면 안된다!
아무리 간선 가중치 값이 적다고 해도!
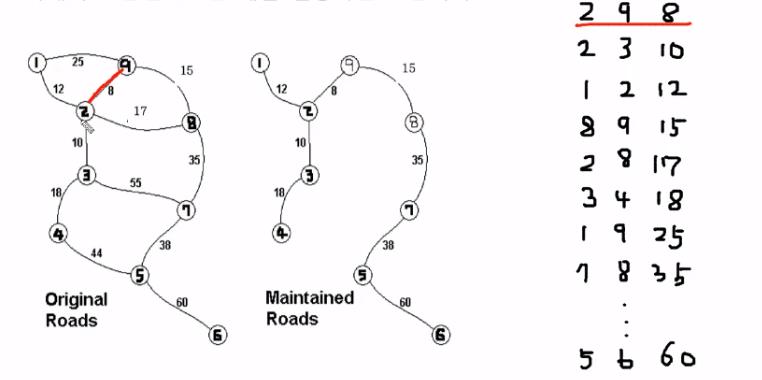
3. 2번 정점과 9번 정점은 최소비용신장트리의 원소로 들어옴
=> 이때 Union & Find로 집합을 만들어서 연결시켜버린다.
4. 2와 3을 연결하는 가중치값 10 인 간선
=> 이 간선을 선택하느냐 마느냐에서 2번 정점을 find로 하고, find 3을 하여
둘이 서로 다른 집합이면 연결한다.
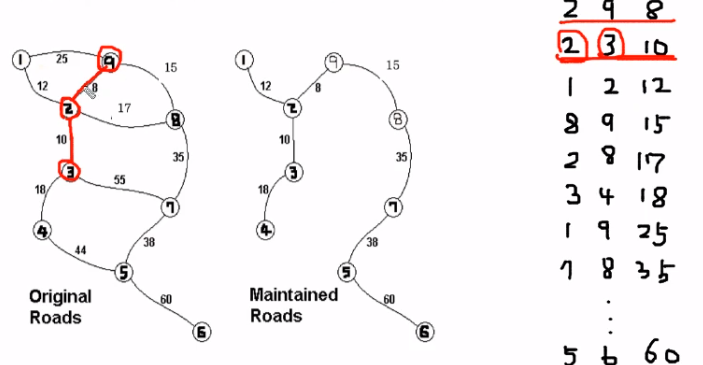
2와 3도 Union 한다.
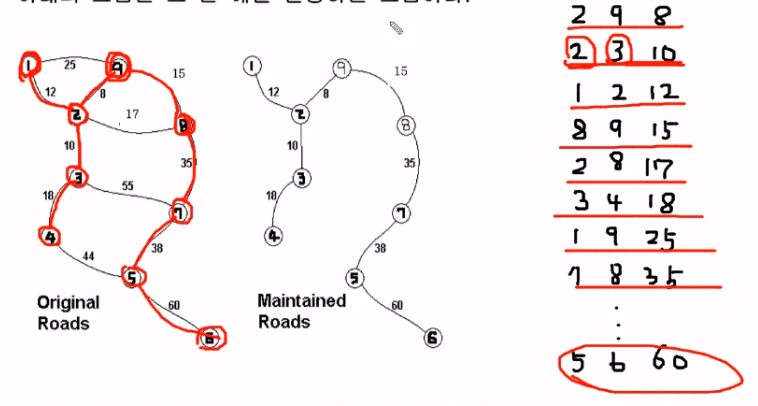
5. 이런식으로 계속 간선값을 누적한다.

6. 이미 2번과 8번 정점은 연결되어 있는 상태이기 때문에 선택하지 않는다.
=> 회로가 되면 안된다! 싸이클을 피해라!
7. find 8 find 9는 이미 트리의 집합의 원소로 되어 있기 때문에 그냥 지나간다.
8.
해설코드
Kruscal Algorithm - Union & Find
최소비용신장트리를 만드는 과정에서 간선의 가중치값을 오름차순으로 하고
회로 없이 만들어 나간 것! 간선이 기준!
//78번 - 원더랜드 Kruskal MST 알고리즘 : Union&Find 활용
#include <stdio.h>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
int unf[1001];
//간선정보 구조체
struct Edge {
int v1;
int v2;
int val;
//생성자
Edge(int a, int b, int c) {
v1 = a;
v2 = b;
val = c;
}
//연산자오버로딩 val 기준 오름차순 정렬
bool operator<(Edge& b) {
return val < b.val;
}
};
int Find(int v) {
//배열의 번호와 안의 값이 일치하는지 보기(연결됨?)
if (v == unf[v]) return v;
else {
return unf[v] = Find(unf[v]); //재귀
}
}
void Union(int a, int b) {
a = Find(a);
b = Find(b);
//연결안되어 있으면 연결시켜줌
if (a != b) unf[a] = b;
}
int main() {
freopen("input.txt", "rt", stdin);
int v, e, a, b, c, cnt = 0, res = 0;
//정보가 많을 때는 구조체를 Vector로 넣기
vector<Edge> Ed;
scanf("%d %d", &v, &e);
//모든 정점을 자기 단독의 집합이라 초기화
for (int i = 1; i <= v; i++) {
unf[i] = i;
}
for (int i = 1; i <= e; i++) {
scanf("%d %d %d", &a, &b, &c);
Ed.push_back((Edge(a, b, c)));
//생성자 호출을 통해 edge형으로 vector에 차례대로 삽입
}
//가중치 값에 의해서 (bool operator) 오름차순 정렬
sort(Ed.begin(), Ed.end());
for (int i = 0; i < e; i++) {
//간선을 선택할거야? find 해봄
int fa = Find(Ed[i].v1);
int fb = Find(Ed[i].v2);
//서로 다른 집합이면 연결(즉 연결안된 상태면)
if (fa != fb) {
res += Ed[i].val;
Union(Ed[i].v1, Ed[i].v2);
}
}
printf("%d\n", res);
return 0;
}
Prim Algorithm - Priority Queue 우선순위큐 활용
간선을 선택 X 임의의 시작 정점을 선택하고 그래프의 연결관계를 버면서 노드를 한개씩 추가해나가는 방법
정점을 하나씩 추가하면서 정점인 n개가 되면 트리가 완성되는 것
1. 임의의 정점을 선택한다.
2. 우선순위큐 - 최소힙 구조를 쓴다.
3. 1번 정점을 출발정점으로 하고 우선순위 큐에 넣는다. 한쌍으로.
1번정점 그리고 간선의 가중치 0의 가중치에서 왔다고 생각해서.
(1, 0) 들어왔다가
우선순위큐이기 때문에 가중치 값이 가장 큰것이 top이다.
이 1번 정점에서 pop하고 빠짐
4. 1번 정점에서 갈 수 있는 그래프가 2개가 있다. 방향그래프 처럼 생각하라.
1번에서 갈 수 있는 노드 2개를 우선순위 큐에 넣는다.
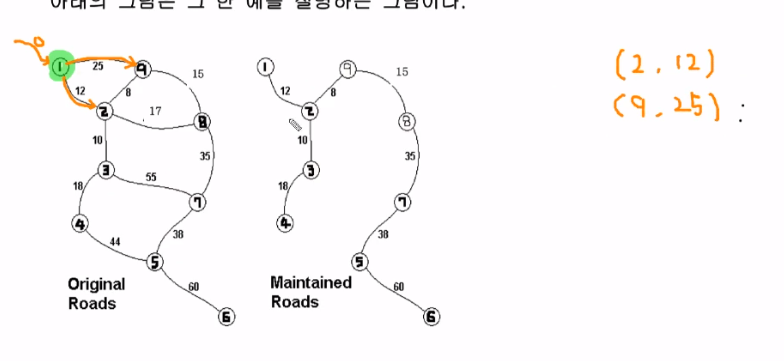
5. 이제 우선순위큐에서 가중치 값이 가장 작은 (2, 12)가 pop하고 나오고 참조된다.
그 다음 2번 정점이 트리의 원소로 추가된다.
6. 이제 2번 노드에서 갈 수 있는 정점들을 우선순위 큐에 다 넣는다.
이 중 최소 힙이기 때문에 가중치가 가장 작은 것이 참조 된다.
그 다음에 우선순위 큐에서 pop하고, 9번 노드가 추가된다.
이때 간선값들은 계속 누적해 놓는 것이다.
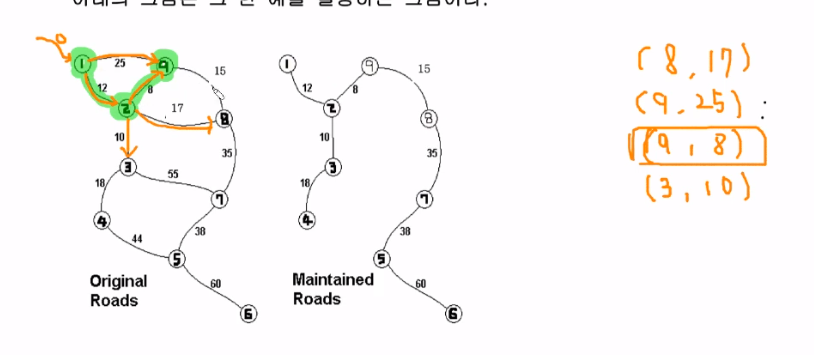

8번 노드가 이미 추가 되어있으면 선택하면 안된다!!
pop만하고 지나간다, 값을 누적하지 않고.
그래서 정점번호들을 check배열을 만들어서 정점을 꼭 체크를 해야한다.
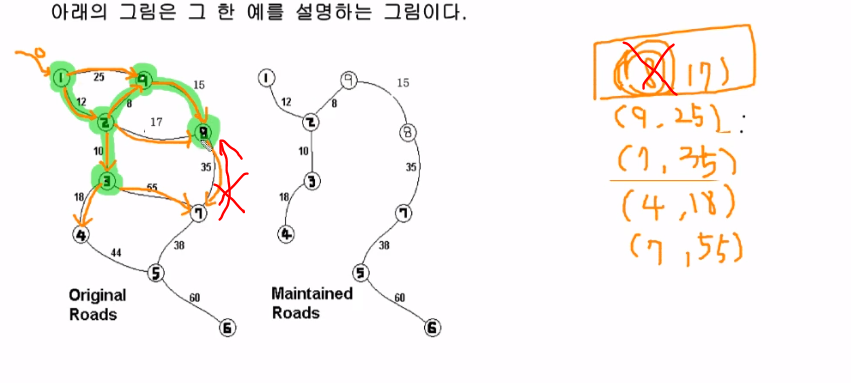
그 다음 우선순위 큐에서 18이 제일 수가 적어서 4번 노드를 추가 한다.
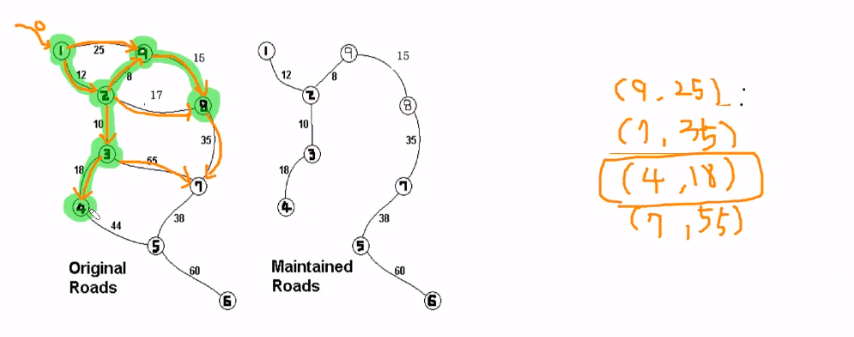
*우선순위 큐에서는 가중치 기준 제일 낮은 것을 참조하고 pop한다.
*이미 지나간 정점은 넣지 않는다.
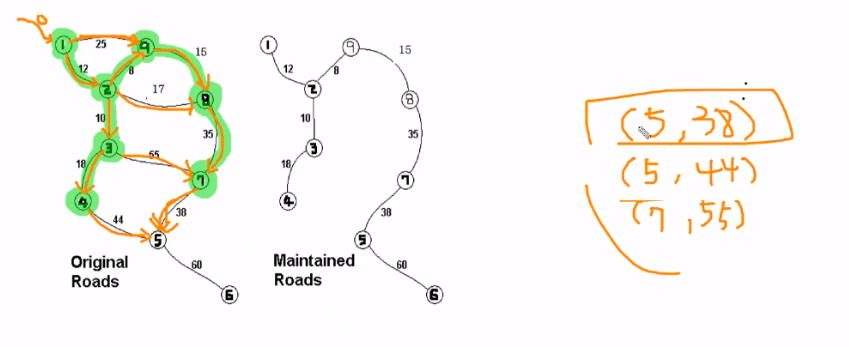

마지막 보면,
참조값이 44로 제일 낮은 5번 노드 이미 참조됨
그 다음 참조값이 낮은 55인 7번 노드도 참조됨
38의 참조값이 제일 낮은 5번 노드는 참조가 안됨 => 참조 후 6번 노드 넣고 pop,
큐가 비면 이 알고리즘은 끝
//79번 원더랜드 - 우선순위큐 활용
//78번 - 원더랜드 Kruskal MST 알고리즘 : Union&Find 활용
#include <stdio.h>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
int ch[30];
struct Edge {
int e; //노드
int val; //간선 가중치값
//생성자로 입력한 (노드, 간선값) 대입
Edge(int a, int b) {
e = a;
val = b;
}
bool operator<(const Edge &b)const {
return val > b.val; //최소힙으로 리턴됨
//부등호 방향을 < 로 하면 최대힙으로 리턴됨
}
};
int main() {
freopen("input.txt", "rt", stdin);
priority_queue<Edge> Q;
//가중치 인전리스트 때문에 만듬
vector<pair<int, int> > map[30];
int n, m, a, b, c, res = 0;
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &a, &b, &c);
//무방향 가중치 인접리스트 a->b, b->a 가능
map[a].push_back(make_pair(b, c));
map[b].push_back(make_pair(a, c));
}
//알고리즘 시작
Q.push(Edge(1, 0)); //임의의 출발 정점
while (!Q.empty()) {
//2번째 바퀴부터 큐에서 가장 작은 값 참조
Edge tmp = Q.top();
Q.pop(); //최초 (1, 0) 날라감
int v = tmp.e;
int cost = tmp.val;
//이미 지나간 원소이냐 아니냐 확인
if (ch[v] == 0) {
res += cost;
ch[v] = 1;
for (int i = 0; i < map[v].size(); i++) {
Q.push(Edge(map[v][i].first, map[v][i].second));
//first : 정점번호 secnd : 간선값
//Edge는 생성자고 이 값을 push 해준다.
}
}
}
printf("%d\n", res);
return 0;
}
'[알고리즘] 문제풀이 연습' 카테고리의 다른 글
| [알골90제] 81번 - 벨만포드 알고리즘(다시풀기) (0) | 2019.08.23 |
|---|---|
| [알골90제] 80번 - 다익스트라 알고리즘 (0) | 2019.08.22 |
| [알골90제] 73/74번 - 최대힙/최소힙 : 우선순위큐 (0) | 2019.08.20 |
| [알골90제] 72번 - 공주구하기 (큐) (0) | 2019.08.20 |
| [알골90제] 71번 - 송아지 찾기 (BFS: 상태트리탐색) (0) | 2019.08.09 |